ADSimDetector

author:

Mark Rivers (University of Chicago), John Hammonds (Argonne National Laboratory)

Table of Contents

Introduction

This is an EPICS areaDetector driver for a simulated area detector. The simulation detector is useful as a model for writing real detector drivers. It is also very useful for testing plugins and channel access clients.

This driver inherits from ADDriver. It implements nearly all of the parameters in asynNDArrayDriver.h and in ADArrayDriver.h, with the exception of the file saving parameters, which it does not implement. It also implements a few parameters that are specific to the simulation detector. The simDetector class describes this class in detail.

The writeInt32 and writeFloat64 methods override those in the base class. The driver takes action when new parameters are passed via those interfaces. For example, the ADAcquire parameter (on the asynInt32 interface) is used to turn acquisition (i.e. computing new images) on and off.

Simulation driver specific parameters

The simulation driver-specific parameters are the following:

Parameter Definitions in simDetector.cpp and EPICS Record Definitions in simDetector.template

Description

drvInfo string

EPICS record name

EPICS record type

Gain in the X direction

SIM_GAINX

$(P)$(R)GainX, $(P)$(R)GainX_RBV

ao, ai

Gain in the Y direction

SIM_GAINY

$(P)$(R)GainY, $(P)$(R)GainY_RBV

ao, ai

Gain of the red channel

SIM_GAIN_RED

$(P)$(R)GainRed, $(P)$(R)GainRed_RBV

ao, ai

Gain of the green channel

SIM_GAIN_GREEN

$(P)$(R)GainGreen, $(P)$(R)GainGreen_RBV

ao, ai

Gain of the blue channel

SIM_GAIN_BLUE

$(P)$(R)GainBlue, $(P)$(R)GainBlue_RBV

ao, ai

The offset added to the image.

SIM_OFFSET

$(P)$(R)Offset, $(P)$(R)Offset_RBV

ao, ai

The amount of random noise added to the image.

SIM_NOISE

$(P)$(R)Noise, $(P)$(R)Noise_RBV

ao, ai

Set to 1 to reset image back to initial conditions

RESET_IMAGE

$(P)$(R)Reset, $(P)$(R)Reset_RBV

longout, longin

Sets the simulation mode. Options are:

  • 0: LinearRamp (linear ramp)

  • 1: Peaks (Array of peaks)

  • 2: Sine (Sum or product of sine waves)

  • 3: Offset&Noise (Offset and noise only, fastest mode)

SIM_MODE

$(P)$(R)SimMode, $(P)$(R)SimMode_RBV

mbbo, mbbi

Parameters for Array of Peaks Mode

X location of the first peak centroid

SIM_PEAK_START_X

$(P)$(R)PeakStartX, $(P)$(R)PeakStartX_RBV

longout, longin

Y location of the first peak centroid

SIM_PEAK_START_Y

$(P)$(R)PeakStartY, $(P)$(R)PeakStartY_RBV

longout, longin

X width of the peaks

SIM_PEAK_WIDTH_X

$(P)$(R)PeakWidthX, $(P)$(R)PeakWidthX_RBV

longout, longin

Y width of the peaks

SIM_PEAK_WIDTH_Y

$(P)$(R)PeakWidthY, $(P)$(R)PeakWidthY_RBV

longout, longin

Number of peaks in X direction

SIM_PEAK_NUM_X

$(P)$(R)PeakNumX, $(P)$(R)PeakNumX_RBV

longout, longin

Number of peaks in Y direction

SIM_PEAK_NUM_Y

$(P)$(R)PeakNumY, $(P)$(R)PeakNumY_RBV

longout, longin

X step between peaks

SIM_PEAK_STEP_X

$(P)$(R)PeakStepX, $(P)$(R)PeakStepX_RBV

longout, longin

Y step between peaks

SIM_PEAK_STEP_Y

$(P)$(R)PeakStepY, $(P)$(R)PeakStepY_RBV

longout, longin

Used to introduce randomness in the peak height. If non-zero then each gaussian peak in the array is assigned a scaling factor:

scalingFactor = 1.0 + (rand() % peakVariation + 1) / 100.0

SIM_PEAK_HEIGHT_VARIATION

$(P)$(R)PeakVariation, $(P)$(R)PeakVariation_RBV

longout, longin

Parameters for Sine Mode

The operation to use to combine XSine1 and XSine2. Choices are:

  • 0: Add

  • 1: Multiply

SIM_XSIN_OPERATION

$(P)$(R)XSineOperation, $(P)$(R)XSineOperation_RBV

mbbo, mbbi

The operation to use to combine YSine1 and YSine2. Choices are:

  • 0: Add

  • 1: Multiply

SIM_YSIN_OPERATION

$(P)$(R)YSineOperation, $(P)$(R)YSineOperation_RBV

mbbo, mbbi

The amplitude of the sine wave. There is a record for each of the 4 sine waves: XSine1, XSine2, YSine1, YSine2.

SIM_[X,Y]SIN[1,2]_AMPLITUDE

$(P)$(R)[X,Y]Sine[1,2]Amplitude, $(P)$(R)[X,Y]Sine[1,2]Amplitude_RBV

ao, ai

The frequency of the sine wave. A frequency of 1 means there is one complete period of the sine wave across the image in the X or Y direction. There is a record for each of the 4 sine waves: XSine1, XSine2, YSine1, YSine2.

SIM_[X,Y]SIN[1,2]_FREQUENCY

$(P)$(R)[X,Y]Sine[1,2]Frequency, $(P)$(R)[X,Y]Sine[1,2]Frequency_RBV

ao, ai

The phase of the sine wave in degrees. A phase of 90 is the same as a cosine wave. There is a record for each of the 4 sine waves: XSine1, XSine2, YSine1, YSine2.

SIM_[X,Y]SIN[1,2]_PHASE

$(P)$(R)[X,Y]Sine[1,2]Phase, $(P)$(R)[X,Y]Sine[1,2]Phase_RBV

ao, ai

Simulation Modes

Linear Ramp

For monochrome images (NDColorMode = NDColorModeMono) the simulation driver initially sets the image[i, j] = i * SimGainX + j * SimGainY * ADGain * ADAcquireTime * 1000. Thus the image is a linear ramp in the X and Y directions, with the gains in each direction being detector- specific parameters. Each subsquent acquisition increments each pixel value by ADGain * ADAcquireTime * 1000. Thus if ADGain = 1 and ADAcquireTime = .001 second then the pixels are incremented by 1. If the array is an unsigned 8 or 16 bit integer then the pixels will overflow and wrap around to 0 after some period of time. This gives the appearance of bands that appear to move with time. The slope of the bands and their periodicity can be adjusted by changing the gains and acquire times.

For color images (NDColorMode = NDColorModeRGB1/RGB2/RGB3) there are 3 images computed, one each for the red, green and blue channels. Each image is computed with the same algorithm as for the monochrome case, except each is multiplied by its appropriate gain factor (SimGainRed, SimGainGreen, SimGainBlue). Thus if each of these color gains is 1.0 the color image will be identical to the monochrome image, but if the color gains are different from each other then image will have color bands.

Array of Peaks

For monochrome images, an array of gaussian peaks is produced. The user specifies the start location for the first peak in PeakStartX & PeakStartY. The size of the peak is controlled by PeakWidthX and PeakWidthY. The array is specified by giving the number of peaks in each direction with PeakNumX and PeakNumY and the step size between peak centroids with PeakStepX and PeakStepY. The amplitude of each peak is controlled by SimGainX, SimGainY, and ADGain. If SimGainX = 1, SimGainY = 1, SimNoise = 0, and SimPeakHeightVariation = 0 then the peak height is equal to ADGain, ADGain = 255 would be appropriate for an 8-bit image. Note that data for each peak is only added to the image over a range of four times the PeakWidth in any direction (in the interest of speed).

Dynamic behavior can be introduced into the system by changing PeakVariation and Noise records. PeakVariation introduces variation in the height of each peak in the array and Noise introduces variation in each pixel.

The description for RGB images is the same as for the Linear Ramp. Pixels are computed the same way as for monochrome and there is a separate gain for each color.

Sine

The image is constructed from 2 sine waves in the X direction and 2 sine waves in the Y direction. The amplitude, frequency, and phase of each of the 4 sine waves can be controlled. The two sine waves in each direction can be combined either by addition or by multiplication. There also global offset and noise parameters. Each sine wave is constructed using the following equation:

X/YSine[i] = Amplitude * sin((Count[X,Y] * Gain[X,Y] / Size[X,Y] * Frequency + Phase/360) * 2 * PI)

where

  • Count[X,Y] is an integer counter that increments by 1 for each element of the sine wave for each new image. It reset to 0 when the image is reset with SimResetImage, or when the image dimensions or datatype are changed.

  • Amplitude sets the sine-wave amplitude. The peak-to-peak value is twice this.

  • i is an index that goes from 0 to the image dimension SizeX or SizeY.

  • Gain[X,Y] is GainX or GainY defined above.

  • Size[X,Y] is SizeX or SizeY, the number of pixels in the X or Y direction.

  • Frequency is the sine wave frequency. Frequency = 1 is one full period across the image.

  • Phase is the phase angle in degrees.

There are 4 separate values for Amplitude, Gain, and Frequency, one for each of the 4 sine waves.

If the Frequency is an integer then there will be an integer number of sine wave periods across the image, and these will appear to be stationary from one image to the next. If Frequency is not an integer then there will be a non-integer number of periods across the image, and the sine wave will appear to move from one image to the next. This is because Count[X,Y] is not reset to 0 for each new image.

In monochrome mode the following equation is used to construct each image:

Value[i,j] = Gain * (Offset + (Noise * random) + XSine1[i] (+ or *) XSine2[i] + YSine1[j] (+ or *) YSine2[j])

where

  • Gain is the overall image gain defined in ADBase.template.

  • Noise is the overall noise level in the image.

  • random is a random number in the range -1 to 1 that is different for each pixel in the image.

  • i is an index that goes from 0 to the image dimension SizeX.

  • j is an index that goes from 0 to the image dimension SizeY.

  • XSine1, XSine1, YSine1, YSine2 are the 4 sine waves described above.

  • (+ or -) is either addition or multiplication depending on the value of XSineOperation and YSineOperation described above.

In color mode (NDColorMode = NDColorModeRGB1/RGB2/RGB3) the following equations are used to construct each image:

Red[i,j]   = Gain * GainRed   * (Offset + (Noise * random) + XSine1[i])
Green[i,j] = Gain * GainGreen * (Offset + (Noise * random) + YSine1[j]
Blue[i,j]  = Gain * GainBlue  * (Offset + (Noise * random) + (XSine2[i] + YSine2[j]) / 2))

where the values have the same meaning as for monochrome images, and GainRed, GainGreen, and GainBlue are the same as for Linear Ramp mode explained above. Note that the red image is a single sine wave in the X direction (XSine1), the green image is a single sine wave in the Y direction (YSine1), and the blue image is the sum of XSine2 and YSine2.

Offset

The image is controlled only by the Offset and Noise parameters. This is the fastest mode.

Unsupported standard driver parameters

  • Collect: Number of exposures per image (ADNumExposures)

  • Collect: Trigger mode (ADTriggerMode)

  • File control: No file I/O is supported

Configuration

The simDetector driver is created with the simDetectorConfig command, either from C/C++ or from the EPICS IOC shell:

int simDetectorConfig(const char *portName,
                      int maxSizeX, int maxSizeY, int dataType,
                      int maxBuffers, size_t maxMemory,
                      int priority, int stackSize)

The simDetector-specific fields in this command are:

  • maxSizeX Maximum number of pixels in the X direction for the simulated detector.

  • maxSizeY Maximum number of pixels in the Y direction for the simulated detector.

  • dataType Initial data type of the detector data. These are the enum values for NDDataType_t, i.e.

    • 0: NDInt8

    • 1: NDUInt8

    • 2: NDInt16

    • 3: NDUInt16

    • 4: NDInt32

    • 5: NDUInt32

    • 6: NDFloat32

    • 7: NDFloat64

For details on the meaning of the other parameters to this function refer to the detailed documentation on the simDetectorConfig function in the simDetector.cpp and in the documentation for the constructor for the simDetector class.

Example st.cmd startup file

There an example IOC boot directory and startup script provided with areaDetector: Example st.cmd Startup File.

Screenshots

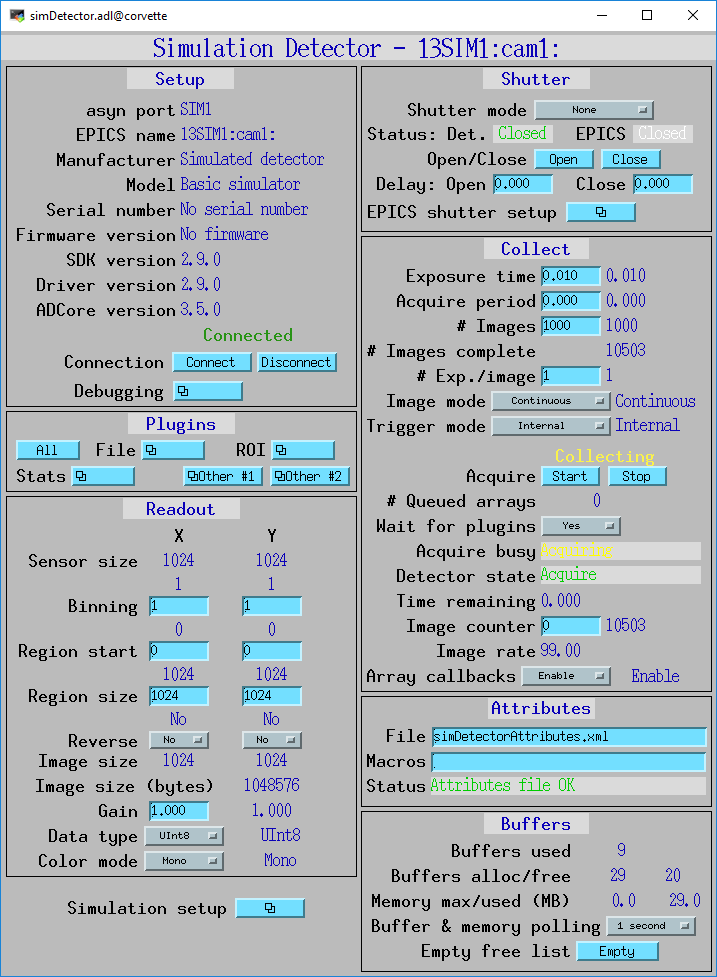
simDetector.adl

The following is the MEDM screen simDetector.adl for the simulation detector.

../_images/simDetector.png

Linear Ramp Mode

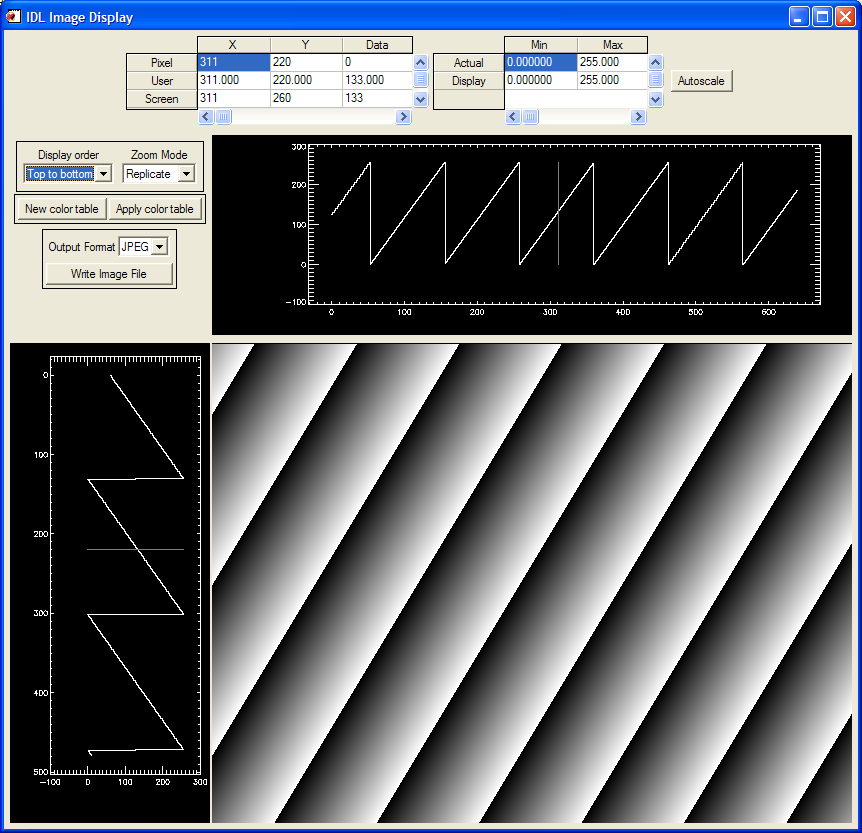
The following is an IDL epics_ad_display screen using image_display to display the simulation detector in monochrome linear ramp mode.

IDL epics_ad_display.pro display of simulation detector in monochrome

../_images/simDetector_image_display.png

Ramp Mode

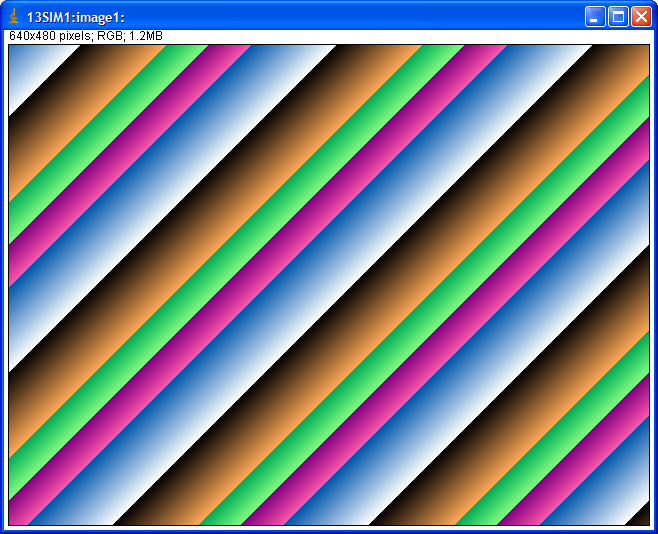
The following is an ImageJ plugin EPICS_AD_Viewer screen displaying the simulation detector in color linear ramp mode.

ImageJ EPICS_AD_Viewer display of simulation detector in color linear

../_images/simDetector_ImageJ_display.png

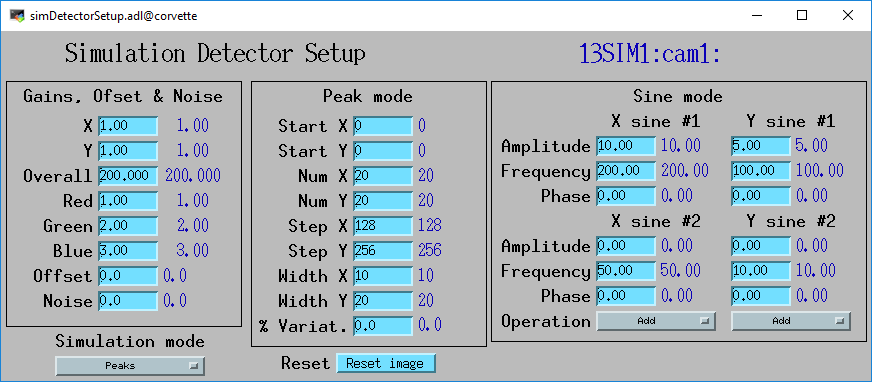
Simulation setup screen with Peaks mode selected

This is an example of the MEDM screen that provides access to the specific parameters for the simulation detector. In this case Peaks mode is selected.

../_images/simDetectorSetupPeaks.png

ImageJ display with the above Peaks mode parameters

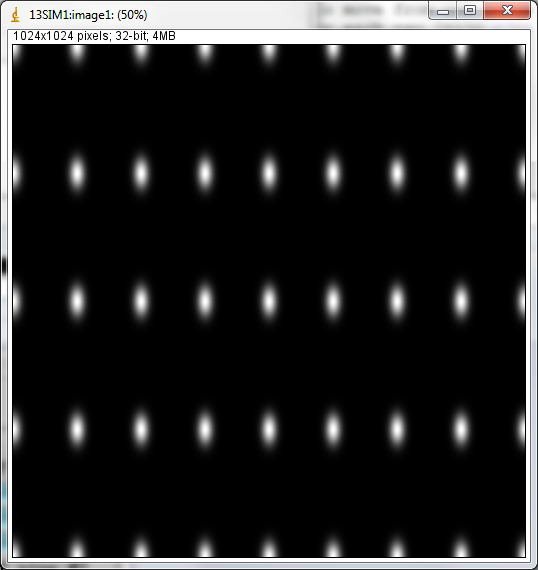
../_images/simDetectorImagePeaks.png

Simulation setup screen with simple Sine mode setup

This is a simple example of Sine mode. The XSine1 frequency is 2 and the YSine1 frequency is 4. The Sine2 amplitudes are zero, so there is a single sine wave in each direction.

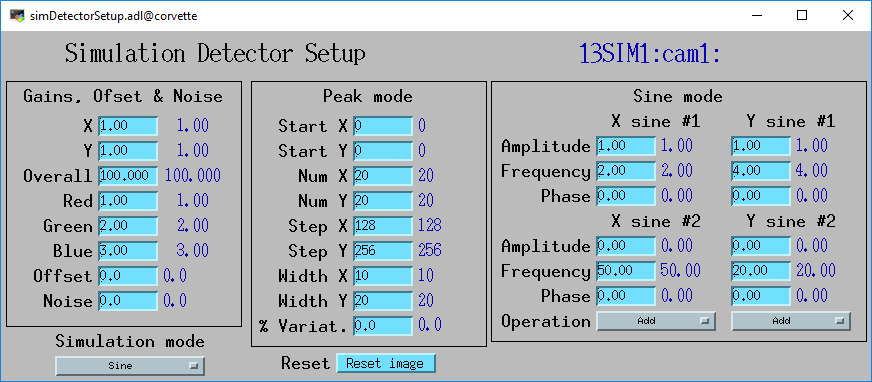
../_images/simDetectorSetupSimpleSine.png

ImageJ display with the above simple Sine mode parameters

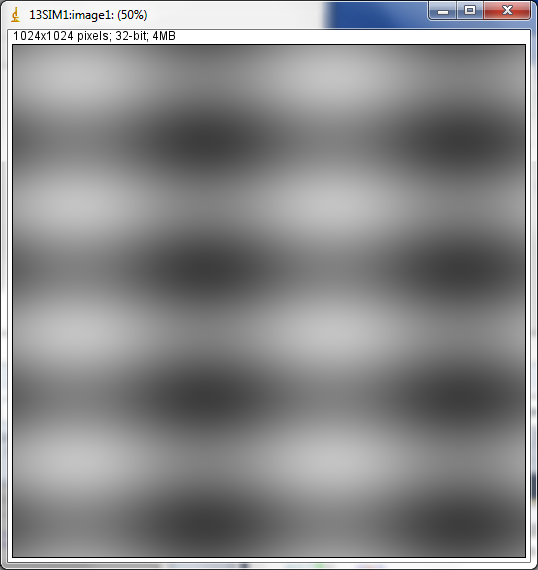
../_images/simDetectorImageSimpleSine.png

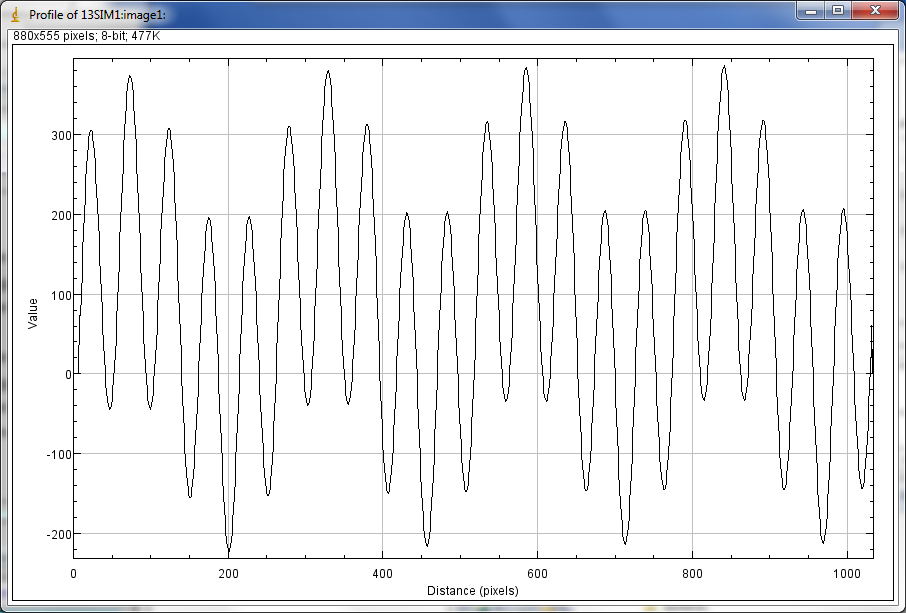
This is a complex example of Sine mode. There are 2 sine waves in each direction, with multiplication in X and addition in Y.

Simulation setup screen with complex Sine mode parameters

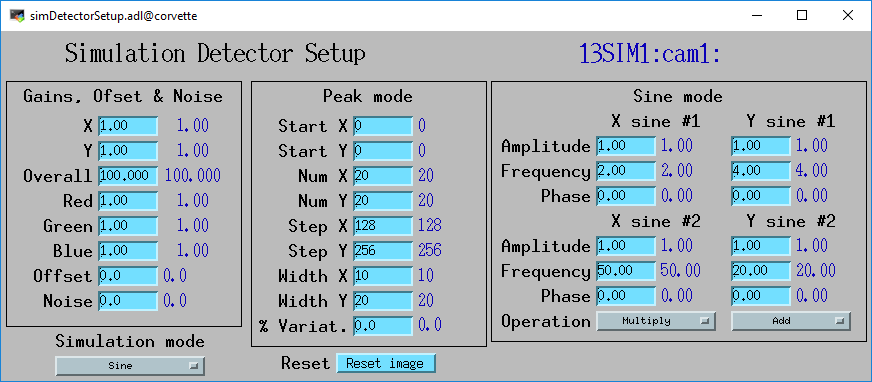
../_images/simDetectorSetupComplexSine.png

ImageJ display with the above complex Sine mode parameters

../_images/simDetectorImageComplexSine.png

ImageJ X profile with the above complex Sine mode parameters.

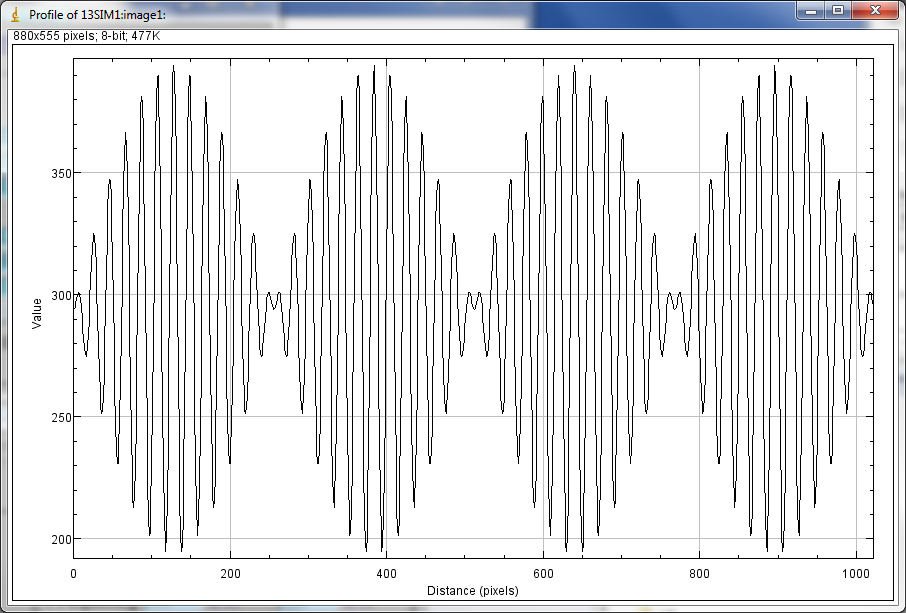
../_images/simDetectorXProfileComplexSine.png

ImageJ Y profile with the above complex Sine mode parameters.

../_images/simDetectorYProfileComplexSine.png

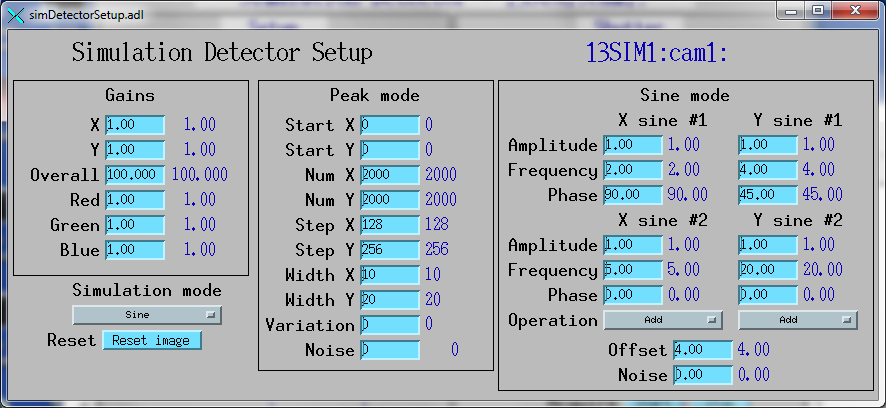
Simulation setup screen with Sine mode parameters in RGB1 color mode

This is a example of Sine mode in RGB1 color mode.

  • The red signal is controlled by a horizontal sine wave with a frequency of 2 and a phase of 90 degrees.

  • The green signal is controlled by a vertical sine wave with a frequency of 4 and a phase of 45 degrees.

  • The blue signal is controlled by the sum of sine waves in the horizontal with a frequency of 5 and in the vertical with a frequency of 20.

../_images/simDetectorSetupColorSine.png

ImageJ display with the above color Sine mode parameters.

../_images/simDetectorImageColorSine.png